
「判断推理」はできるけど、「数的推理」は苦手だし嫌い。

「数的推理」を捨てるのはヤバイ気がするし……。
公務員試験を受験する皆さま!
こんな悩みをお持ちではないでしょうか?
この記事では、どうすれば「数的推理」をマスター出来るか、基本から応用まで徹底解説いたします。
ぜひ参考にして、「数的推理」の苦手意識から開放されてください!
苦手意識の強い数的推理ですが、出題パターンを理解すれば最短1ヶ月で得点源に変えられます。
その最短ルートを実現してくれるのが、出題傾向に完全対応した「Studying(スタディング)」の公務員講座です。
※ 無料体験だけでも「どこから手をつければいいか」がハッキリします。
迷ったらまず1本、講義動画を見てみてください。
📘 数的推理とは?出題範囲と職種ごとの傾向を分かりやすく解説
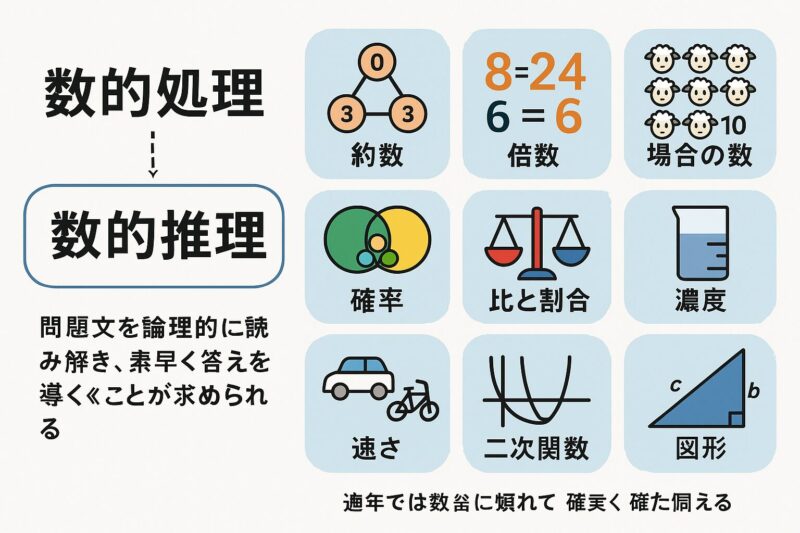
数的推理とは、公務員試験の「数的処理」科目の中の一分野で、中学数学の知識を使って論理的に問題を解く力が問われます。 文章や図、条件を読み解き、短時間で正確に解答を導き出すスキルが求められるため、苦手意識を持つ受験生も少なくありません。
💡 こんな内容が出題されます
- ・約数・倍数、整数、数列
- ・割合・比・濃度・利益・記数法
- ・確率、場合の数
- ・速さ、時間、距離、仕事算、ニュートン算
- ・図形(面積・体積・角度・三角比・円・立体)
- ・その他文章題(集合、年齢、平均、魔方陣など)
※ いずれも中学〜高校初期レベルの数学で対応可能です
これらの出題は「知識」だけでなく、「スピードと正確さ」がカギ。 だからこそ、出題傾向の把握とパターン別の訓練が合否を分けます。
📊 主な職種ごとの出題数(数的推理)
| 職種 | 出題数 | 図形問題の有無 |
|---|---|---|
| 国家一般職 | 約8問 | ◯(1〜2問) |
| 東京都 | 約5問 | ◯(1〜2問) |
| 特別区 | 約6問 | ◯(1〜2問) |
| 地方上級 | 約6問 | ◯(1〜2問) |
| 裁判所事務官 | 約6問 | ◯(図形2問) |
| 市役所 | 約5問 | ◯(1問) |
※ 職種によって出題数は異なりますが、どこも判断推理と並ぶ“柱”として問われます。
📌 結論: 数的推理は出題数が多く、捨てると合格がかなり遠のく重要単元です。 苦手でも「出題パターン」を知って対策すれば、最短1ヶ月で得点源にできます。
※判断推理の効率的な勉強法については、こちらの記事で詳しく解説しています。
📘 数的推理が苦手でも大丈夫! 無料体験で「わかる!」を実感しませんか?
スマホでスキマ時間に学べて、出題パターンを動画で“サクッと理解”。
まずは無料体験で、難しい数的推理が“解ける感覚”を体験してみてください。
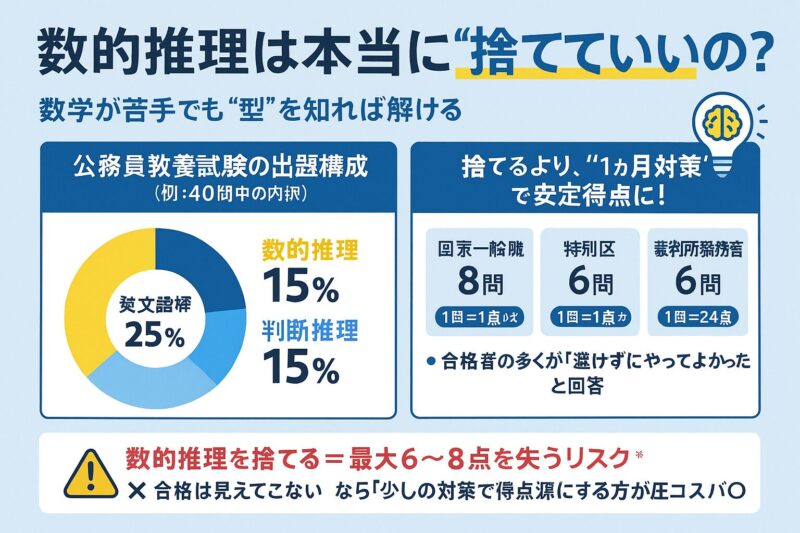
⚠️ 数的推理は捨ててもいい?苦手な人が落ちないための判断基準とは
「どうしても数的推理が苦手…。いっそ捨ててもいいかな?」
そう考えたことのある受験生は、決して少なくありません。
💡 ですが、結論から言えば「捨てるのは危険」です。
数的推理は、判断推理と並んで出題数が多い重要単元。
多くの職種で全体の15〜20%前後を占めるため、対策しないとそもそも合格点に届きません。
📊 主な職種別|数的推理の出題数
- ・国家一般職:8問(全体の約20%)
- ・特別区、地方上級:5〜6問(判断推理と同数)
- ・裁判所事務官:6問(図形含む)
- ・市役所:5問前後
※ 1問=1点。数的推理だけで6点前後=合格ラインの1/4以上に相当
公務員試験では満点は不要ですが、逆に6〜7割を確実に取る必要があります。
その中で数的推理を捨ててしまうと…他で8〜9割の高得点が必要に。これはかなり非現実的です。
✅ 特に、判断推理・数的推理・資料解釈の3本柱は「教養試験の得点源」としてセットで攻略すべき項目です。
「数学アレルギーだから無理…」と感じるかもしれませんが、数的推理は
「出題パターンを覚える」だけで解ける問題が多数あります。
捨てるのではなく、“攻略可能な科目”として割り切って対策するのが合格者のやり方です。
※ 難しい問題ほど“動画で見ると一発でわかる”ことも多いです
✅ 数的推理が苦手な人向け!得点に直結する解き方のコツ
公務員試験では1問あたりの平均時間は3〜4分です。
このような短時間で解答にたどり着くためには、
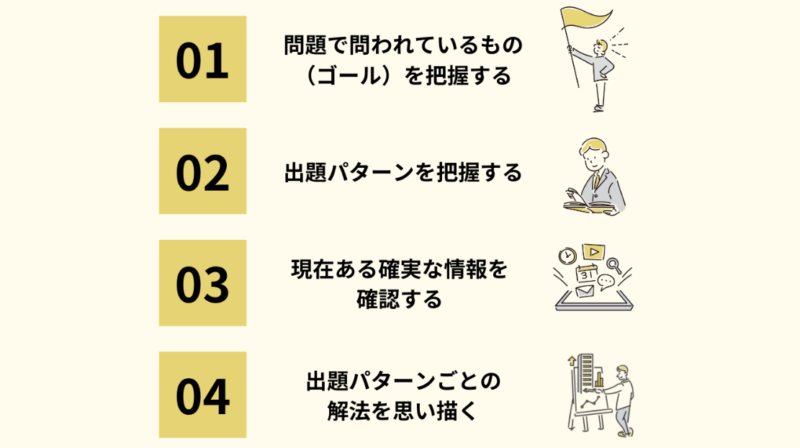
↑これが必須です。
そのため、「解法パターンの暗記」と「作業を素早く行うための練習」が必要です。
「数的推理」に限らず、数的処理の勉強に必要なのは知識と反復練習というのは、ここから来ているわけです。
・出題パターンを確認する
・出題パターンの典型的な解法を暗記
・解法がパッと出るまで問題を解きまくる
・時間を測りながら解く
🔍 出題パターンの見極め方|数的推理でミスを減らす第一歩
1つ目が、出題パターンを確認するです。
ここがかなり重要で、点数が伸びない方に共通しているところだと思います。
問題を解く際に、まずは問題を読みますよね。
その時に、すぐに解法を思い浮かべるのではなく、まずは下記表のどの出題パターンに当てはまるのかを確認することが大切です。
なぜ、出題パターンの確認が大切かというと、
出題パターンには典型的な解法が存在するから
ジャンルを問わない莫大な量の解法を覚えるよりも、出題パターンの解法を覚えた方がはるかに効率が良いですし、解く時間も早くなります。
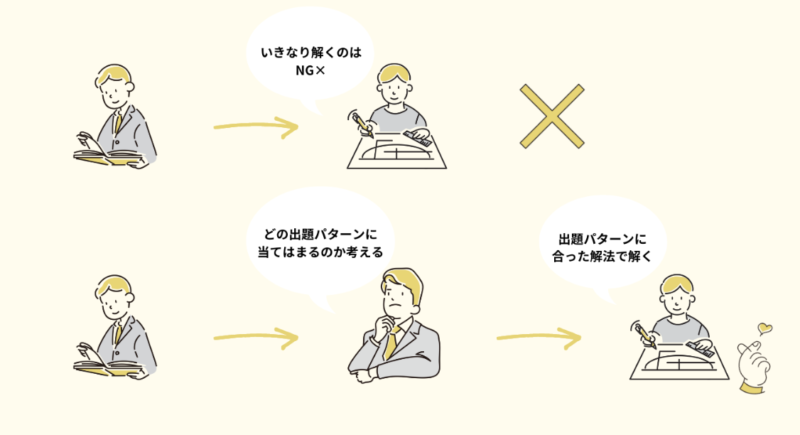
さらに、問題集は出題パターンごとに問題が固まっているため、出題パターンを日頃の勉強で意識しないことが多いんです。
本番は、どの順番でどのような問題が出るかわかりませんからね。
まずは出題パターンの確認!ここを意識してみてください!
💡 頻出パターンはコレ!数的推理の解法を効率よく覚えるコツ
2つ目が、出題パターンの典型的な解法の暗記です。
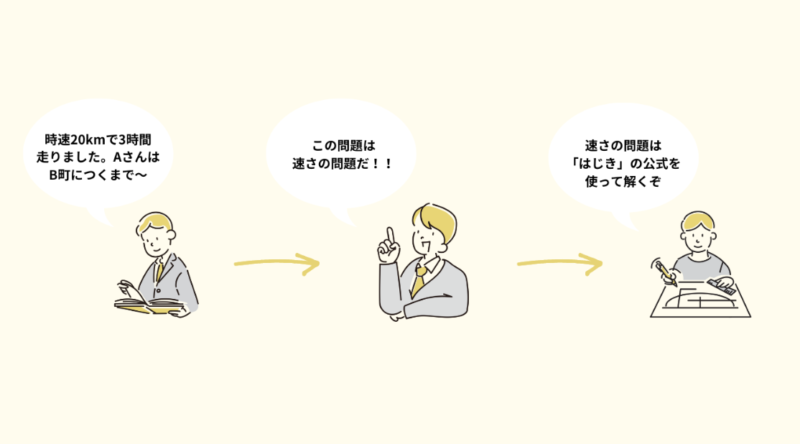
画像の通り、数的推理には出題パターンごとに典型的な解法が存在します。まずは、その解法を覚えること!
・頻出問題に絞る!範囲を広げすぎない!
・問題文のキーワードと解法を結びつける!
この2つを意識するだけ!
ここの意識の差で点数が伸びるか伸びないかが決まってきます!
よくありがちなのが「あれもこれもと暗記の範囲を広げすぎてしまうこと」
公務員試験は過去に出題された類似問題が多く出題されます。そのため、頻出問題に絞って深く学習した方が圧倒的に効率が良く点数が伸びます!
「問題文のキーワードと解法を結びつける」については、次の章で実際の問題を使って解説します!
🔁 解法を“瞬時に思い出す”ための反復練習法とは?
3つ目は、時間を測りながら解くです。
公務員試験は全40問〜50問出題され、その問題数を「2時間30分」で解く必要があります。
単純計算、1問にかけられる時間は3分ほど!
この短い時間の間に
・問題の読解
・出題パターンの確認
・解法の把握
・解く手順
などを考えて答えを導き出すわけです。
さらに、本番は独特な雰囲気と緊張感で時間感覚が麻痺します。日頃から時間感覚を意識して解いておくことが大切です。
⏱ 試験本番を想定した時間管理|1問3分で解く練習法
4つ目が、問題演習を繰り返すです。
あとは、①〜③を意識しながら、ひたすら問題演習を繰り返すだけ!
僕個人の意見ですが、最低でも3周は同じ問題集を解く必要があると考えています。
解法が浮かぶ問題に関しては、もう一度解く必要はなく「問題をみる → 正解までの手順を頭の中で思い浮かべる」これだけでOKです。
必要に応じて4周、5周と回数を増やしていきながら対応していきましょう。
「数的推理って何パターンもあって覚えきれない…」
「問題を見ても、どの解法を使えばいいかピンと来ない…」
- 💡 出題パターンを分類して、要点だけ効率よく学べる
- 🔄 公式や解法の「使いどころ」が動画でスッと理解できる
- 📱 スマホだけで復習OK!スキマ時間でもパターンが定着
- 💬 迷ったら講義で“どこで間違えたか”をすぐ振り返り可能
✅ 【頻出公式!】脳に残る!数的推理公式の覚え方《5ステップ》
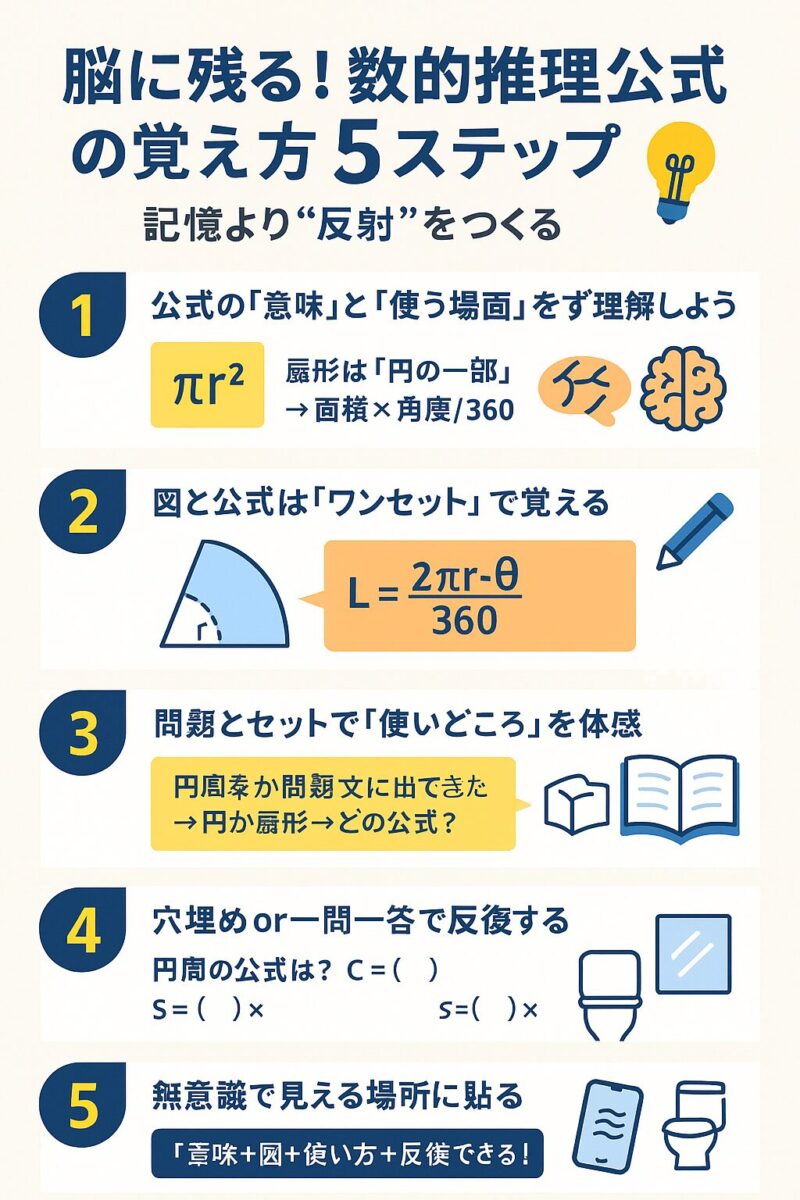
「公式が覚えられない…」
「覚えてもすぐ忘れる…」
そんなあなたにこそ試してほしいのが、記憶より“反射”をつくる5ステップ法です。
① 公式の「意味」と「使う場面」をまず理解しよう
✘ ただ丸暗記 → ❌
✅ なぜそうなるか、どこで使うか → ⭕
🧠 例:
円の面積 πr² を「半径×半径×円周率」として覚えるだけではNG。
「“扇形”は“円の一部” → 面積×角度/360にする」ように、背景と使い道をセットでメモしておくのが大切です。
② 図と公式は“ワンセット”で覚える(視覚記憶法)
図と公式をセットにすることで、“思い出せる”ではなく“思い浮かぶ”に変わります。
✍ 例えば:
扇形の図に《L = 2πr × θ/360》と直接書き込んで、ビジュアルと数式を同時に記憶します。
📌 ポイント:
- 図を見たら公式が思い出せる
- 公式を見たら図の形が浮かぶ
= 応用力も高まります。
③ 問題とセットで「使いどころ」を体感
公式は「どこで使うか」が分かれば、忘れません。
📘 例:
問題文に「円周率」「半径」「中心角」が出てきたら…
→「これは円か扇形だな」→「あの公式だ」と、逆引きでも活用できる力がつきます。
④ 穴埋め or 一問一答で反復する(=アウトプット)
書いて覚える、声に出す、問題で使う。これが一番定着します。
📝 例題:
「円周の公式は?」→ C = ( )
「扇形の面積は?」→ πr² × ( )
📅 ポイント:
- 3日間で5周が効果的(時間より“回数”重視)
- 2回目3回目こそ「覚えてる?」の確認タイミング!
⑤ 無意識で見える場所に貼る(パッシブ記憶)
📱 スマホのロック画面
🚽 トイレの壁
🪞 洗面所の鏡
📖 手帳・ノートの1ページ目
👉 苦手な公式こそ、“見る回数”を味方にするのが最強です。
🧠 「目にする回数 × 短い思考」で、記憶は脳に刷り込まれます。
🔁 まとめ:記憶より「反射」をつくろう
公式は、“頑張って覚える”より、“自然に出てくる状態”を目指すのが正解。
「意味+図+使い方+反復」= 得点できる公式力!
まずはこの5ステップを試して、あなたの“公式アレルギー”を解消していきましょう!
\ 数的推理が苦手な方 必見! /
「公式が覚えられない…」
「どの公式を使うか分からない…」
そんな悩みを1冊のPDFでまるっと解決!
公式の図解・用途・練習問題を
1ページずつ丁寧にまとめました。
- ✅ 図付きで公式の意味がひと目でわかる
- ✅ 「どういう問題で使うか?」を一言解説
- ✅ 穴埋め練習で反射的に使える力がつく
- ✅ スマホでも印刷でも使いやすいシンプル設計
※ 印刷して書き込み用にもおすすめです。
📚 数的推理の過去問対策|分野別の例題&解き方を徹底解説
ここでは各項目ごとの例題と解き方を紹介します。
上記で説明した解き方のコツを参考にしながら繰り返し解くことをおすすめします。
倍数と約数
例題①
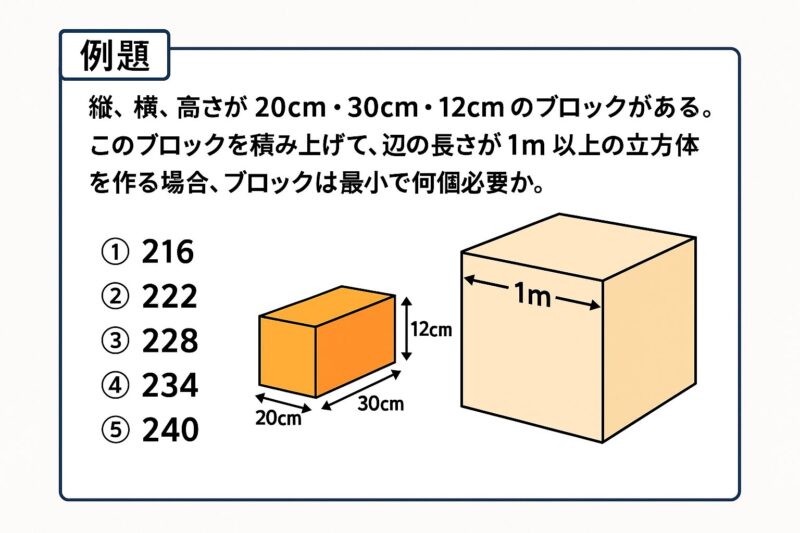
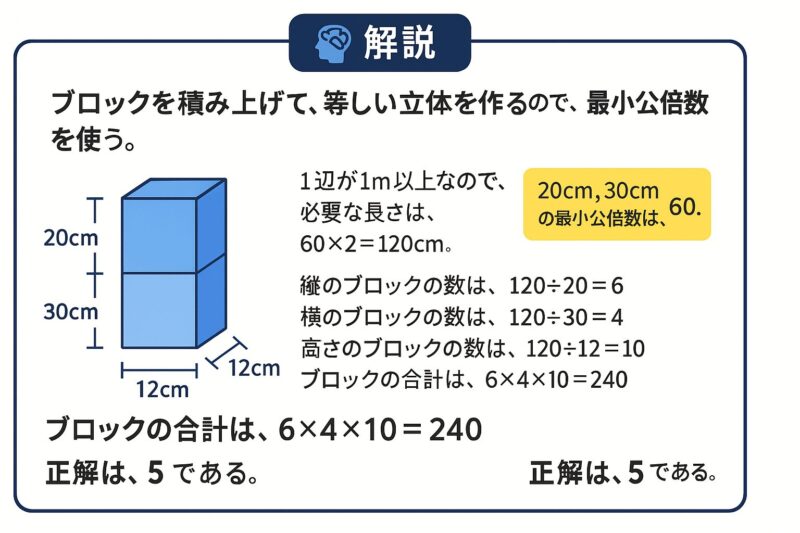
例題②
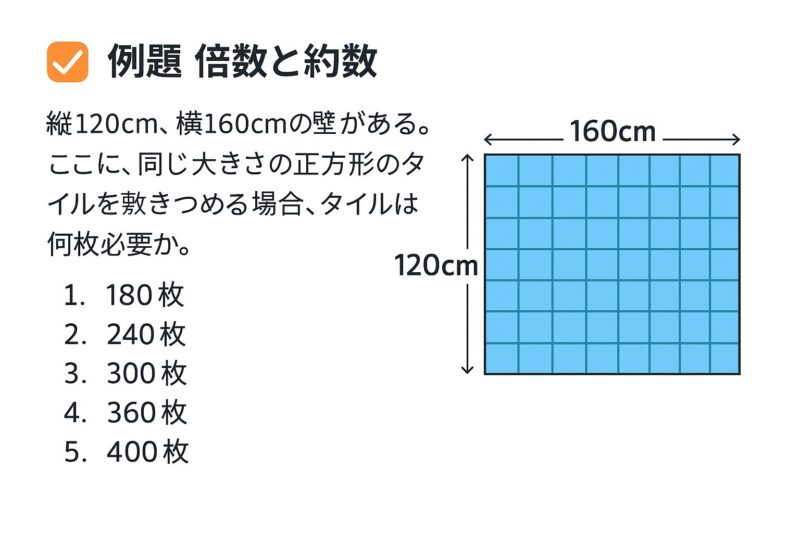
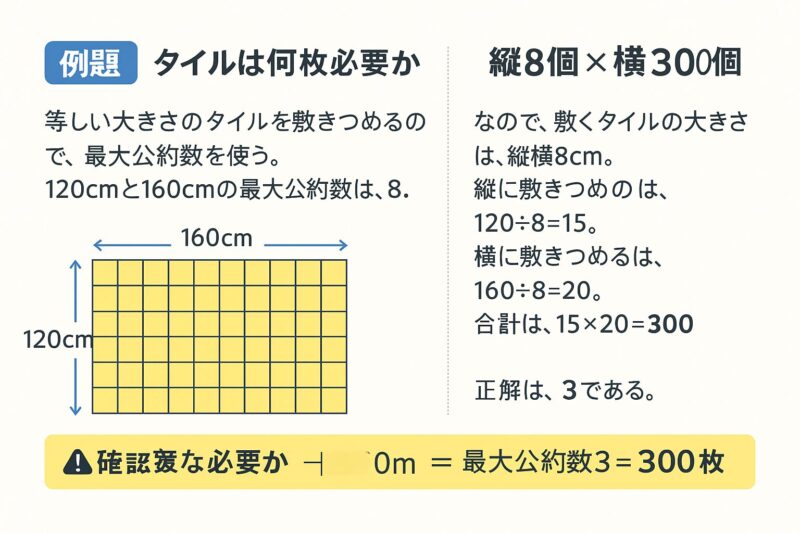
例題③

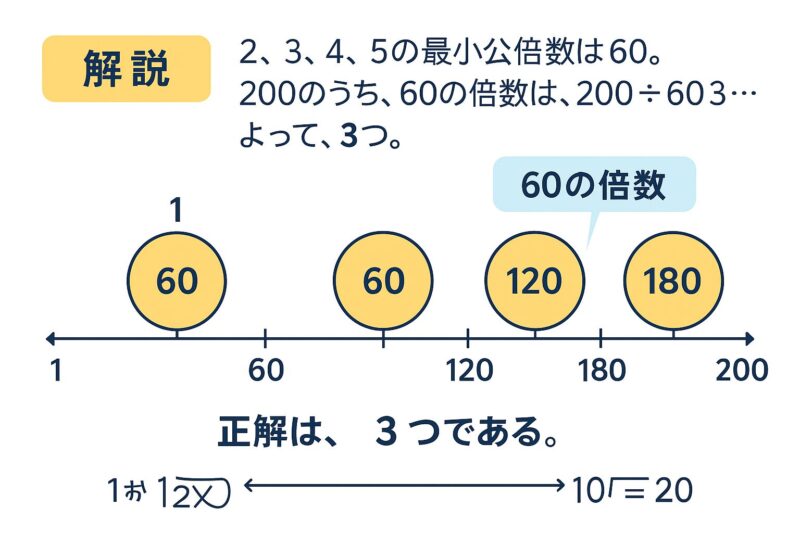
整数
例題①
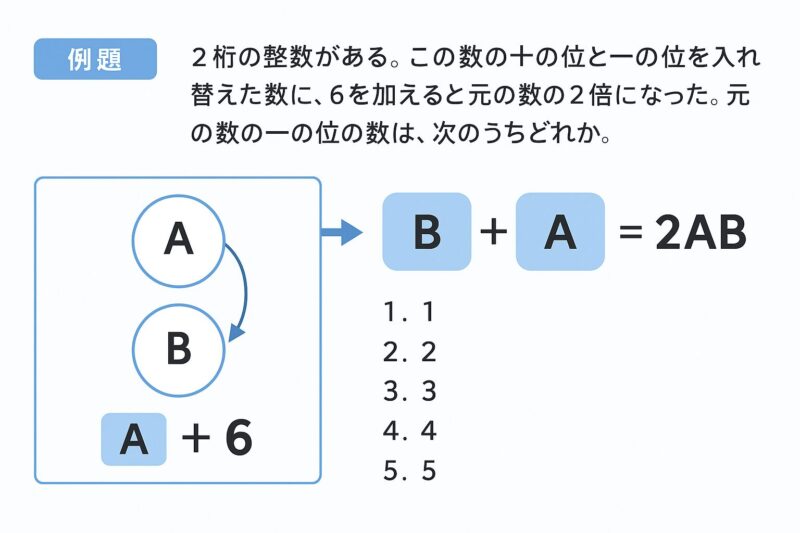
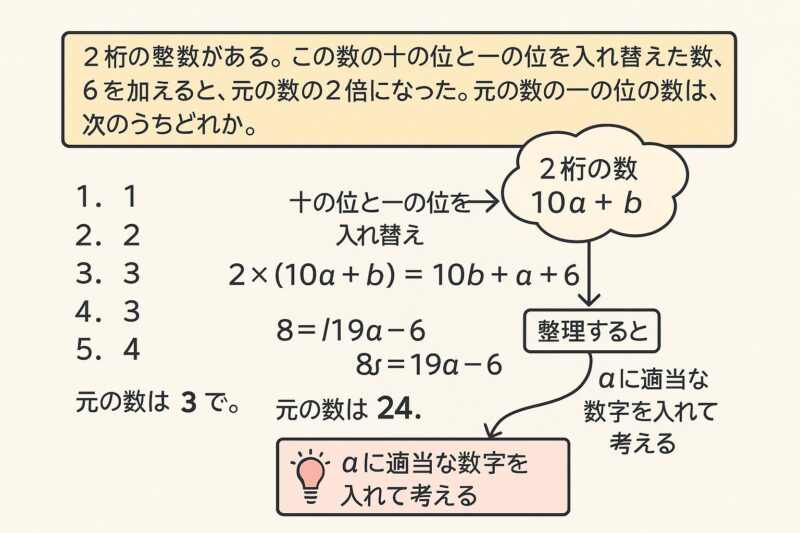
例題②
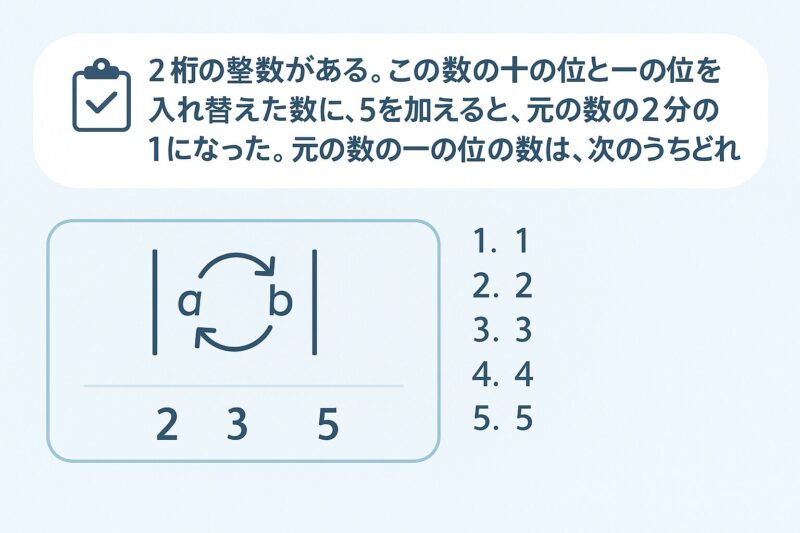
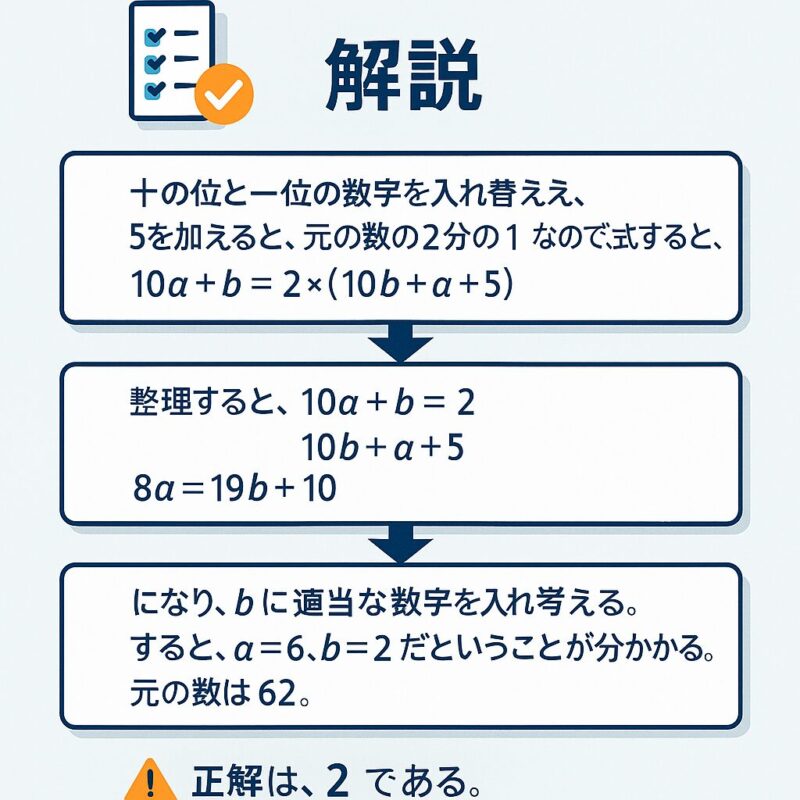
例題③


数の性質
例題①


例題②
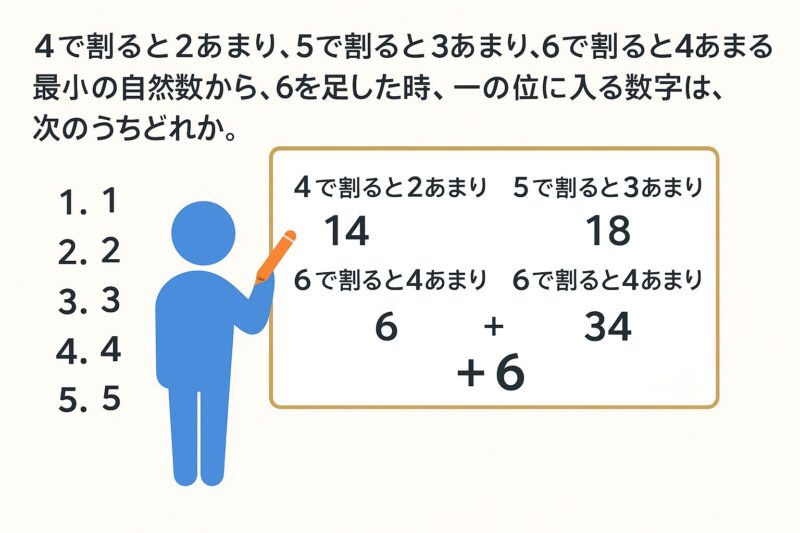
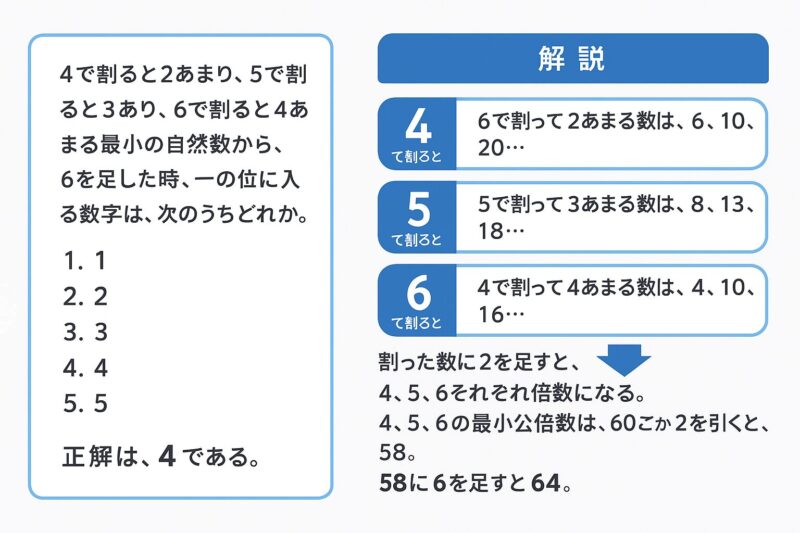
例題③


方程式
例題①
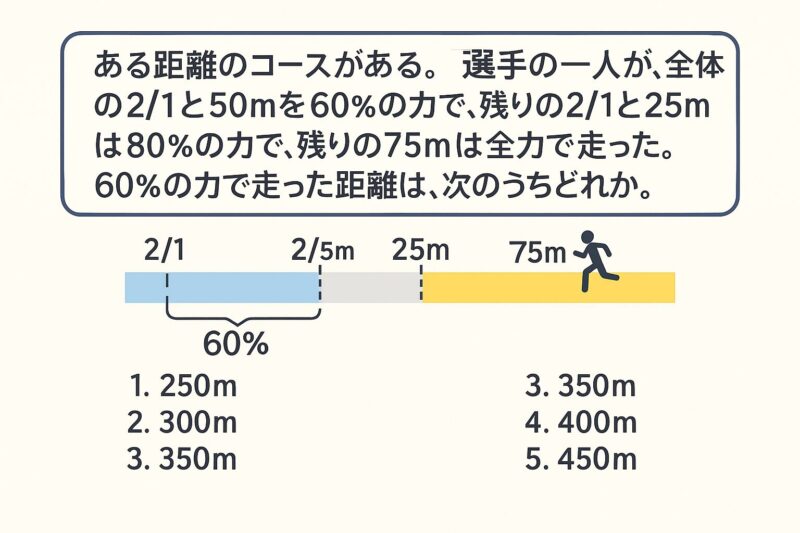
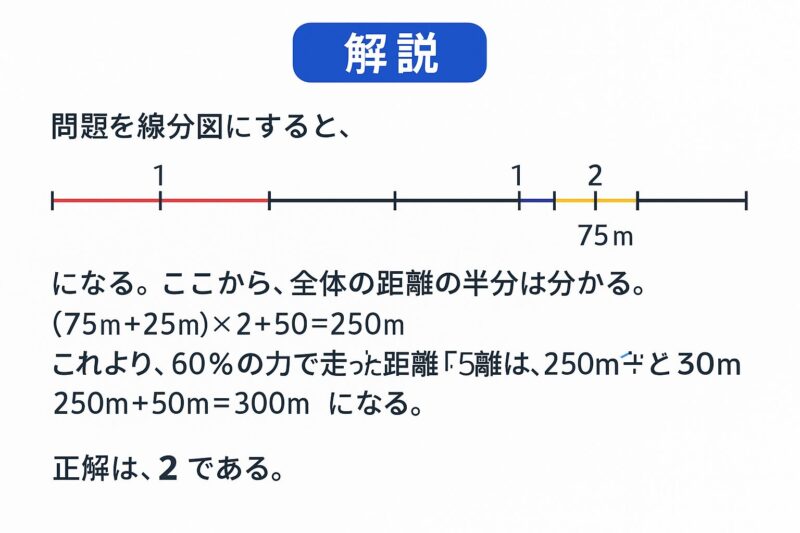
例題②


例題③
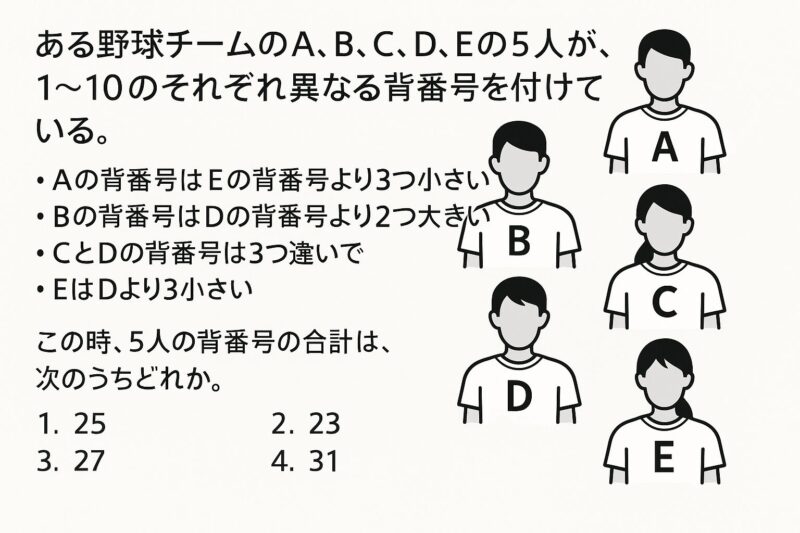

割合
例題①


例題②


例題③


濃度
例題①

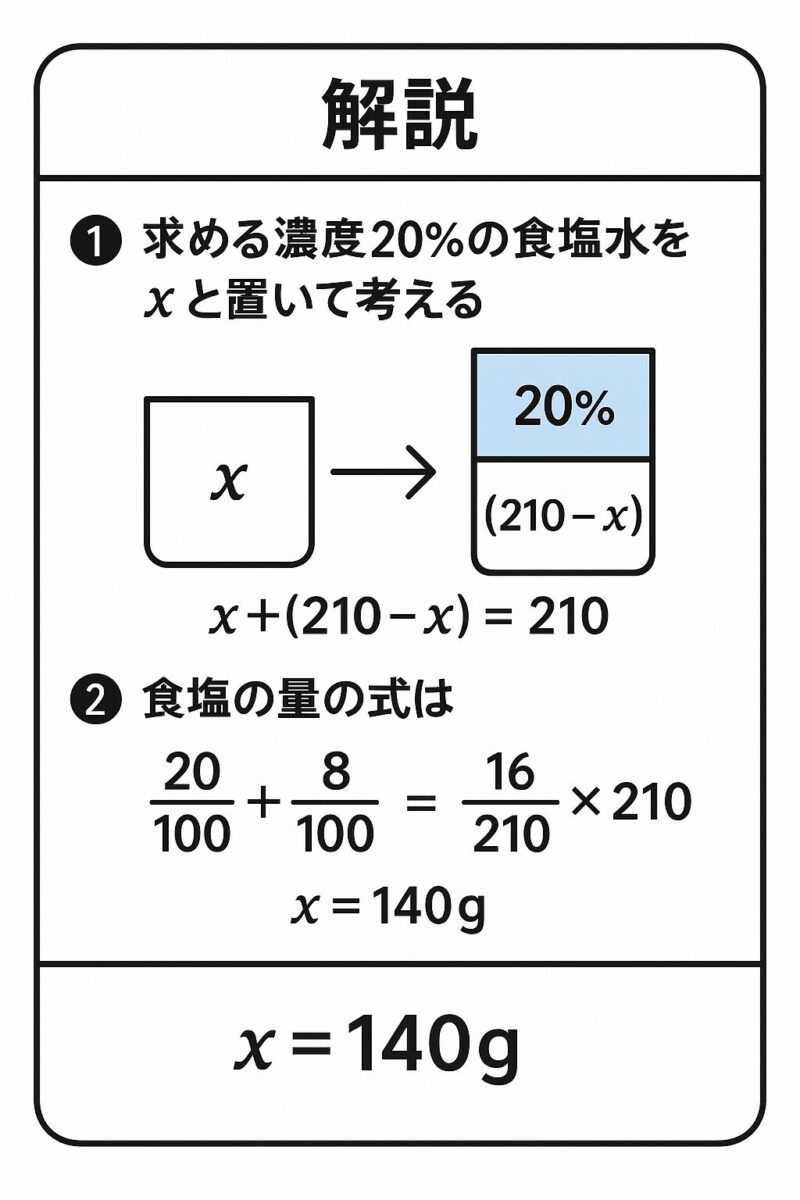
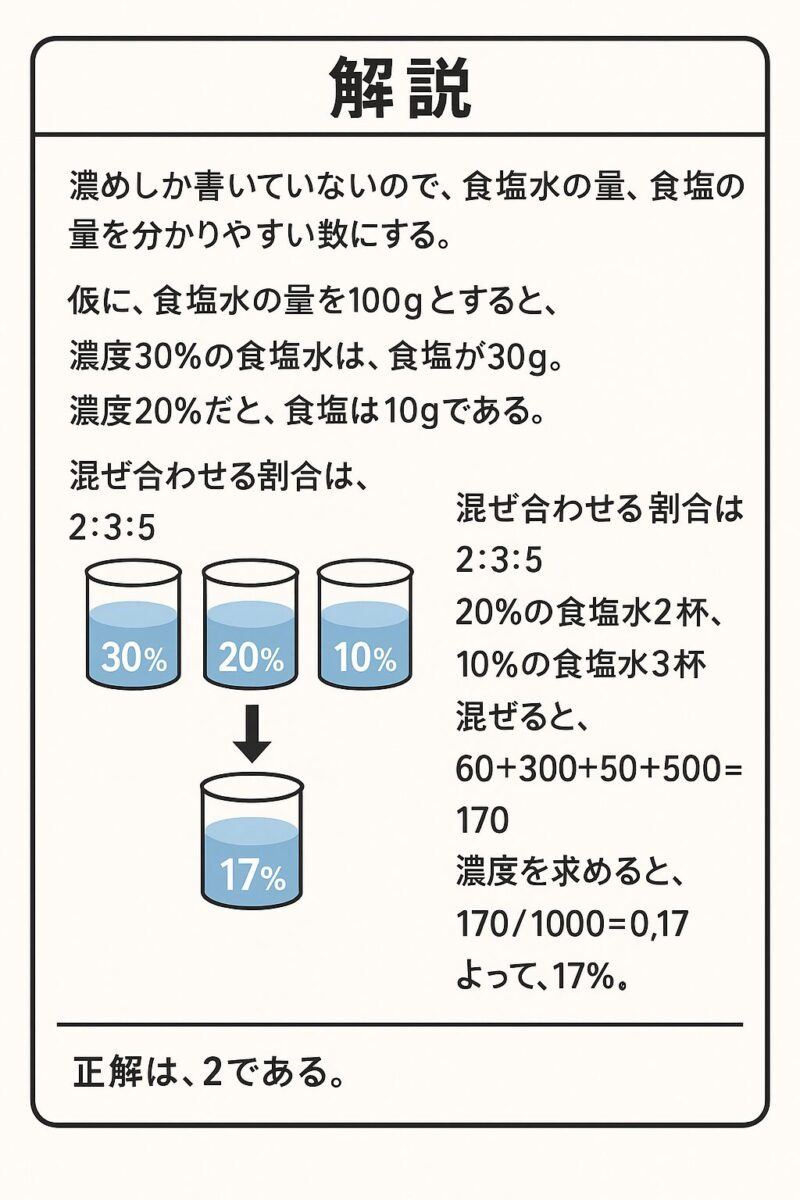
例題②


例題③

速度
例題①

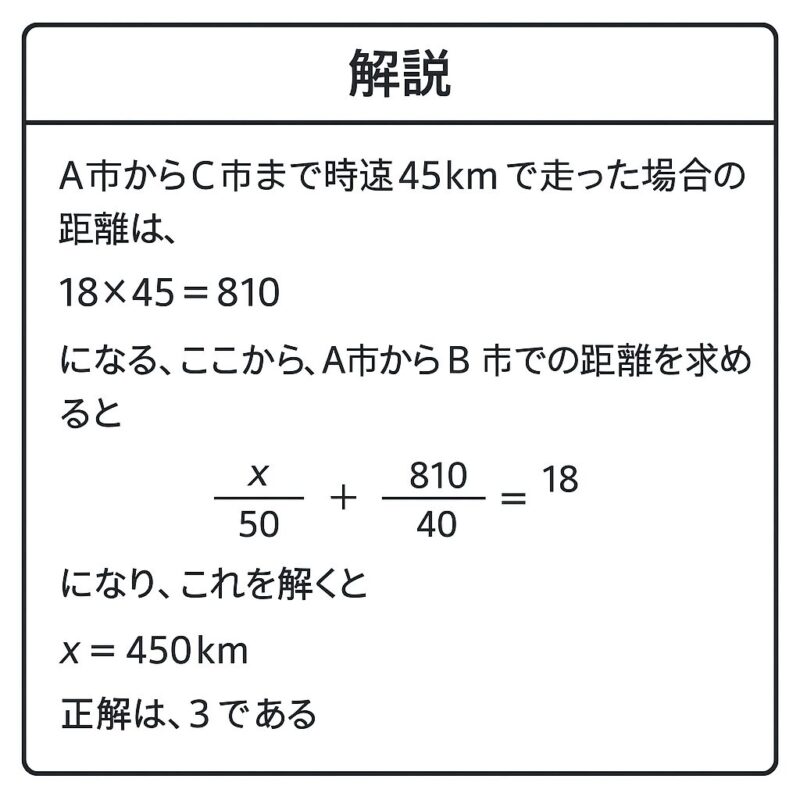
例題②

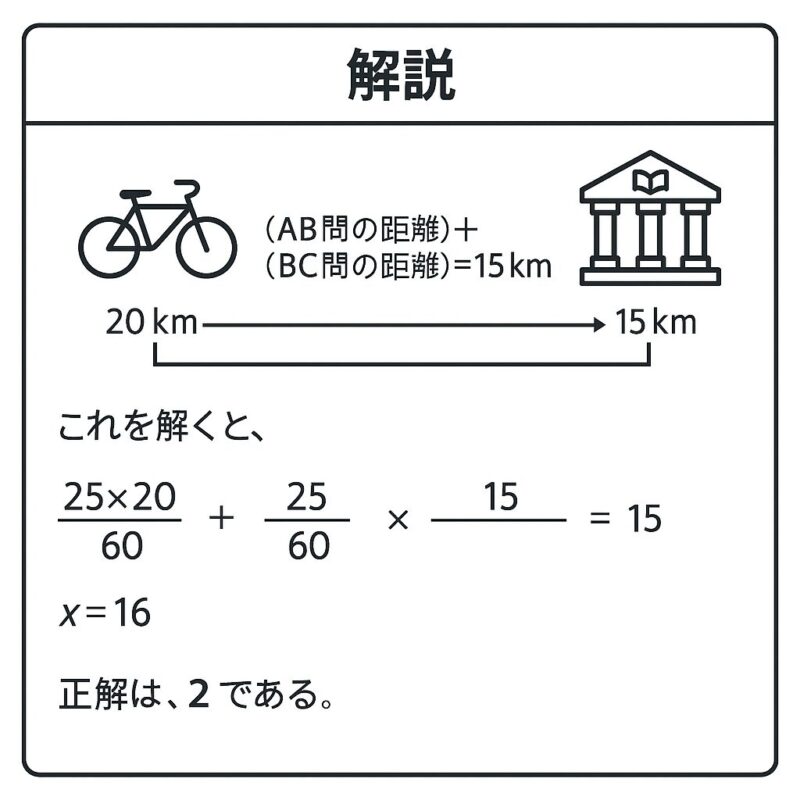
例題③


場合の数
例題①
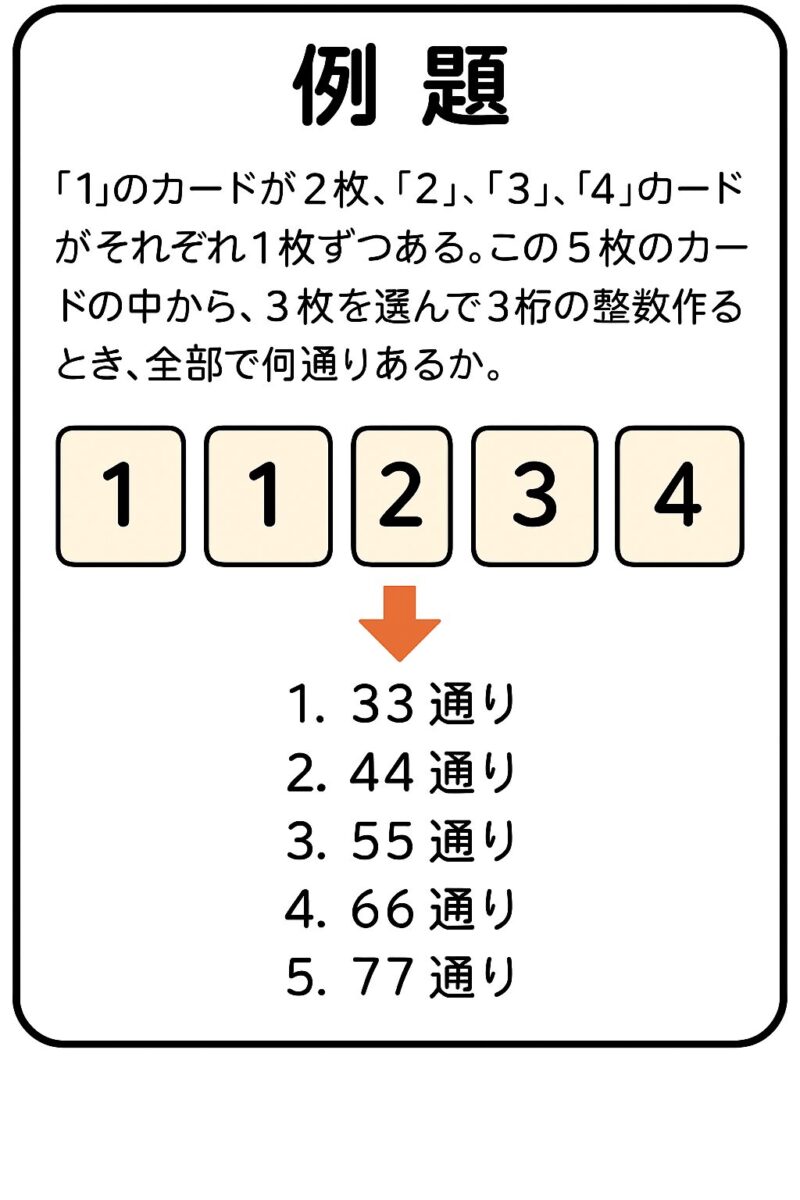
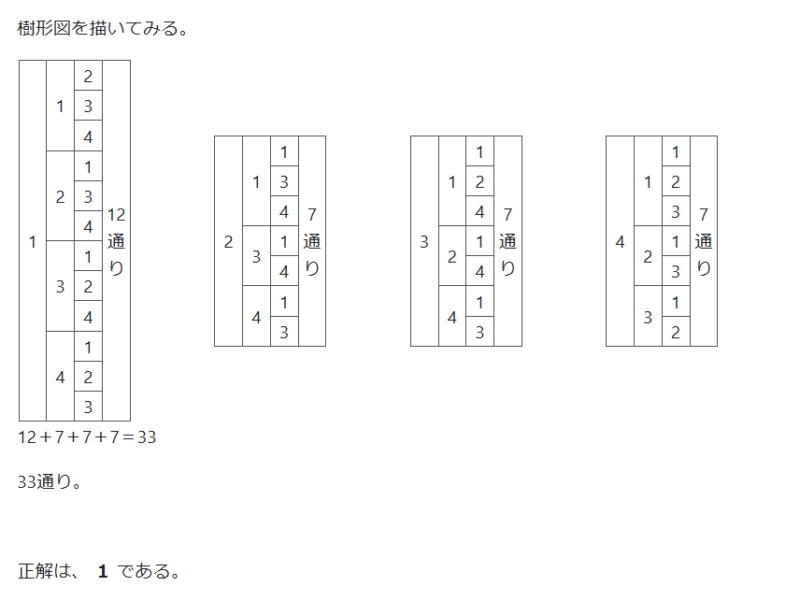
例題②


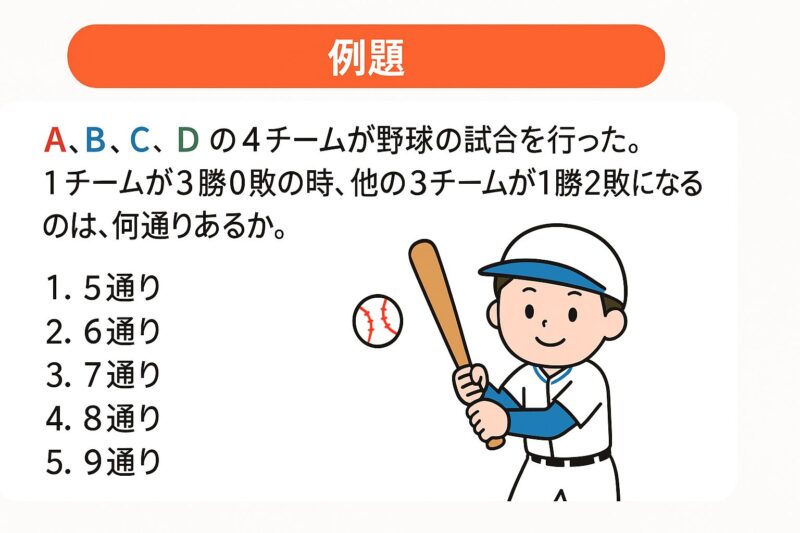
例題③
Q1. 数的推理の勉強経験は?
Q2. あなたの生活スタイルに近いのは?
Q3. 勉強で重視したいポイントは?
❓ よくある質問(FAQ)
A. まずは出題パターンを知ることが最重要です。やみくもに問題を解くより、「これはどのパターンの問題なのか」を分類しながら学ぶことで、効率よく基礎が固まります。講義や参考書で全体像をつかんだ後、過去問演習に移るのがベストです。
A. 一度立ち止まり、図を書いてみたり、具体的な数字を当てはめてみるのがおすすめです。それでも難しい場合は、似たパターンの解説を見て“流れ”をつかむのが効果的です。繰り返しになりますが、「理解できない=センスがない」ではなく「解法にまだ慣れていないだけ」です。
A. 1日30分〜1時間の学習を継続すれば、1〜2ヶ月で安定して得点できる受験生が多いです。重要なのは「1回で完璧に理解しようとしないこと」と「苦手な単元ほど反復すること」です。解ける問題から始めて“成功体験”を積むことがモチベーション維持にもつながります。
A. 少なくとも3周は必要と考えてください。1周目は解法を理解する、2周目は覚えた解法を使えるか確認する、3周目でスピードと精度を高めるイメージです。間違えた問題には付箋やマークをつけて、そこだけ5周でも6周でも繰り返しましょう。
A. 結論から言えば、捨てるのは危険です。試験では判断推理とほぼ同じくらい出題されるため、数的推理を捨てると合格ラインを超えるのが非常に難しくなります。苦手な人ほど「型」を身につければ急激に点数が伸びやすい科目ですので、むしろコスパの良い対策対象です。
✅ 数的推理は「得点源」にできる!だからこそ最初の一歩が大切
数的推理は、最初こそ難しく感じるかもしれません。
でも、出題パターンさえ理解すれば、反復と解法整理で“確実な得点源”に変えられる単元です。
実際、これまで「数学は大の苦手だった…」という受験生の多くが、
Studyingのような講座を活用することで、
- ✅ 1ヶ月で問題の見極めができるように
- ✅ 解法が“反射的”に浮かぶように
- ✅ 苦手だった数的推理が 一番の得点源になった という声もあります
📣 もし今「自分にもできるか不安…」と感じているなら、
まずは無料体験で講義を見てみるのが一番確実です。
✅ 苦手を得点源に変える一歩は、「まず試してみること」から始まります。




